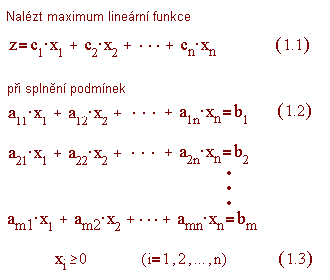
Ulohu linearniho programovani lze matematicky formulovat jako ulohu nalezeni extremu (maxima nebo minima) linearni funkce vice promennych pri vedlejsich podminkach vyjadrenych linearnimi rovnicemi nebo nerovnostmi. Protoze nerovnosti lze prevest na rovnice o vetsim poctu neznamych a reseni uloh minimalizacnich na maximalizacni, formulujeme obecnou ulohu linearniho programovani takto:

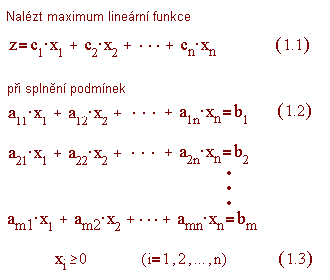
Funkci (1.1), jejiz maximum hledame, nazyvame ucelovou funkci.
 
 

 Rovnice (1.2) jsou vlastni omezeni ulohy.
 
 
 
 
 

 
 Nerovnosti (1.3) se nazyvaji podminkami nezapornosti .
 
 

 Promenne x_i , kde i = 1,2,....,n, charakterizuji objemy procesu, ktere se maji realizovat, ma-li byt dany ukol splnen.
 
 

Uloha linearniho programovani je specialnim pripadem ulohy matematickeho programovani, kde vsechny funkce (tj. ucelova funkce i vsechna vlastnich omezeni) jsou linearni. Vedle linearity funkci se v linearnim programovani predpoklada, ze i vsechny koeficienty ulohy (koeficienty vsech funkci) jsou dana realna cisla.

Ulohu linearniho programovani lze zapsat strucne v maticovem tvaru:

Reseni ulohy linearniho programovani muzeme rozdelit takto:

Pripustne reseni

je reseni soustavy linearnich rovnic (1.2), ktere vyhovuje podminkam nezapornosti (1.3).

Optimalni reseni

je prave takove pripustne reseni, ktere maximalizuje ucelovou funkci (1.1).

Zakladni reseni

je pripustne reseni, ktere ma nejvyse tolik kladnych slozek, kolik je linearne nezavislych rovnic tvoricich vlastni omezeni (1.2) (t.j. v nasem pripade nejvyse m kladnych slozek a nejmene n - m nulovych slozek za predpokladu, ze n > m). Sloupce koeficientu v matici A odpovidajici kladnym slozkam zakladniho reseni jsou linearne nezavislymi vektory.

Degenerovane reseni

je zakladni reseni, ktere ma vice nez n - m nulovych slozek.

Pro reseni uloh linearniho programovani jsou dulezite dve vety:

Veta1.:

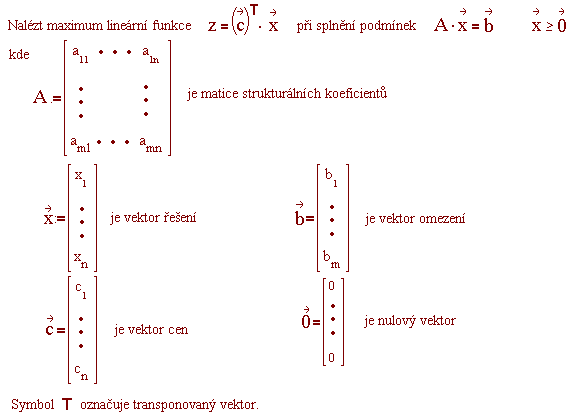
Tato veta je zakladni vetou linearniho programovani.
Ma-li uloha linearniho programovani optimalni reseni, ma tez optimalni reseni zakladni.
To znamena, ze se pri hledani optimalniho reseni muzeme omezit na zakladni reseni, kterych je vzdy konecny pocet, nejvyse rovny kombinacnimu cislu "n nad m".

Veta2.:

Tato veta vyjadruje vlastnost pripustnych reseni ulohy linearniho programovani.
Jsou-li  a  dve pripustna reseni ulohy linearniho programovani, pak i kazda jejich konvexni kombinace, tj. , je pripustne reseni.

Mnozina je konvexni, patri-li do ni s kazdymi dvema body mnoziny i jejich spojnice.
Krajnim bodem mnoziny je bod, ktery nelezi na spojnici jinych dvou bodu mnoziny.

Mnozina pripustnych reseni muze byt:

Pri reseni uloh LP mohou tedy nastat tyto pripady:

- uloha nema optimalni reseni
- uloha ma jedine optimalni reseni (ucelova funkce nabyva optimalni hodnoty v jedinem krajnim bode mnoziny pripustnych reseni)
- uloha ma nekonecne mnoho optimalnich reseni (ucelova funkce nabyva optimalni hodnoty napriklad ve dvou krajnich bodech mnoziny pripustnych reseni a ve vsech bodech spojnice vytvorene temito body)
- ucelova funkce muze na mnozine pripustnych reseni neomezene rust (pri ulohach maximalizacnich) nebo neomezene klesat (pri ulohach minimalizacnich).
 
 

Dopravni uloha byla jednim z prvnich problemu, pri jejichz reseni bylo uspesne pouzito metod linearniho programovani. Ulohu lze resit simplexovou metodou, ale v praxi se uziva specialnich metod (distribucni metody nebo metody vyuzivajici algoritmus z teorie grafu - hledani nejlacinejsiho toku v siti).

 V dopravni uloze jde o prepravu produktu od skupiny dodavatelu ke skupine odberatelu za nejnizsi cenu (nebo po nejkratsi ceste).

Formulace ulohy:

Predpokladame, ze naklady c_ij jsou konstantni, tj. nezavisi na prepravovanem mnozstvi. Dale predpokladejme, ze objem kapacit se rovna objemu pozadavku tj.

a_i  = b_j (1.4)

, neboli pujde o tzv. vyrovnanou dopravni ulohu.

Vsechny udaje muzeme sestavit do prehledne tabulky:

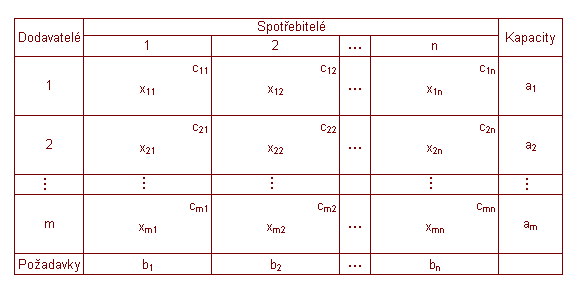
Matematicky model:

Nalezt minimum linearni funkce

z = c_ij . x_ij (1.5)

pri splneni podminek

x_ij = a_i        pro i = 1,2,...,m (1.6)

 x_ij = b_j        pro j = 1,2,...,n                        (1.7)

x_ij  0                 pro i = 1,2,...,m (1.8)

pro j = 1,2,...,n

Vsechna omezeni (1.6) a (1.7) nejsou vzhledem k predpokladu (1.4) nezavisla, jedno vyplyva z ostatnich. Nezavislych omezeni je m + n - 1, tzn., ze zakladni reseni ma nejvyse m + n - 1 kladnych prvku. Dopravni uloha ma vzdy optimalni reseni.

Nevyrovnana dopravni uloha

Existuji i vicerozmerne dopravni ulohy, napr. jde-li zbozi od m dodavatelu k n spotrebitelum pres r meziskladu. Pokud je problem vyrovnan, tj. celkova kapacita dodavatelu je rovna:
    celkovym pozadavkum spotrebitelu
    celkovym kapacitam meziskladu,
lze ulohu resit rozkladem na dve jednorozmerne dopravni ulohy.