The fundamental requirement of IK Limb solver is that the solution be history-independent: the solution has to be based on the goal and other incidental parameters solely at their current states.
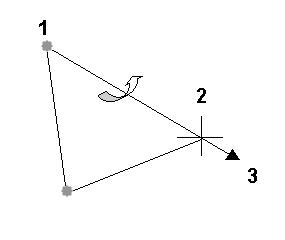
When the positional goal is given for a single chain, there remains an obvious degree of freedom: the rotation about the End Effector Axis (EE Axis). The swivel angle is used to describe this degree of freedom quantitatively.

1. start joint
2. End effector
3. EE axis
LetÆs call the plane passing all the joints the Solver Plane. When joints do not lie on a plane, we will define it to be the plane that (A) passes the Start Joint and End Joint and (B) is closest to the remaining joint in a certain sense.
The Swivel Angle describes the degree of freedom of the Solver Plane and it constrains only the Start Joint.
In order to describe the solver plane in terms of a numerical quantity, we have to agree to what 0 means. Given the end-effector position, where is the Zero (Solver) Plane? The Zero Plane Map takes as the argument EE Axis and produces the normal to the zero plane.
The IK system allows individual solver plug-ins to define their own Zero Plane Maps. When not defined, the IK system provides a default one.
The argument to the Zero Plane Map is a unit vector to give the direction of the EE axis. Equivalently, when the EE slides along the EE axis, the solver plane should be fixed. Therefore, the Zero Plane Map defines a vector field on a sphere. Given a point on the sphere, it produces a tangential unit vector to be interpreted as the normal to the zero plane.
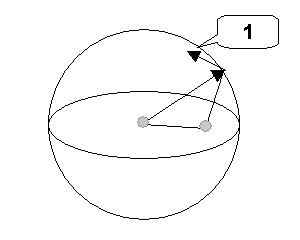
1. Normal to the zero plane
It is a mathematical fact that there does not exist a continuous vector field on a sphere. No matter how hard you try, there will always be a point on the sphere where neighboring vectors change dramatically. This is where the solver plane will flip when the end effector axis approaches to it.
This is because, on one hand, the IK requirement demands us to assign a fixed vector to the singular point. On the other hand, no matter what vector is assigned, it will be dramatically different from some vectors assigned to the neighboring points.
In order to define the Zero Plane Map, we need to define a reference frame for the sphere. This reference frame is intrinsic to the joint chain itself.
A sphere can be defined by the center, the horizontal plane, and the meridian (zero longitude). The center is assigned to the start joint.
The pose when all the joint angles assume preferred angles is particularly important. LetÆs call it the preferred pose.
We use the solver plane at the preferred pose as the horizontal plane. Since the swivel angle is used to control the start joint, the preferred angles at the start joint are not so intrinsic. The solver plane of the preferred pose (except that the start joint) assumes zero angles are also reasonable.
The EE axis defines the meridian. The sphere is now defined as shown in the following figure:
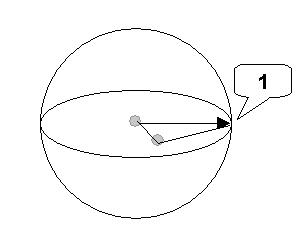
1. EE axis
All the joints assume preferred angles. The Zero Plane Map is to be defined on this sphere.
The API for the plug-in solver to define its own Zero Plane Map in fact takes the EE axis and the normal to the solver plane at the preferred pose:
virtual const IKSys::ZeroPlaneMap*
GetZeroPlaneMap(const Point3& a0, const Point3& n0) const
where a0 and n0 are the EE axis and solver plane at the preferred pose, respectively. Object of ZeroPlaneMap is a function that assigns a plane normal to each point on the sphere.
When not provided by plug-in solvers, (the IK Limb Solver itself is implemented as a plug-in solver) the IK system will provide a default one. This map is defined by the following rules:
A: For each point on the equator, the intersection of the horizontal plane and the sphere, the normal vector is defined as the vertical vector, pointing to the same direction as the normal of the solver plane at the preferred pose.
B: For any point on the sphere other than the north or south poles, there is a great circle that passes the point and the north, south poles. This circle hits the equator at two points. One point is closer to the given point. The normal vector at the given point is defined as derived from moving tangentially the normal at the closer point on the equator along the great circle to the point.
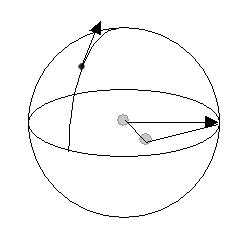
Obviously, this method wonÆt extend to the north or south poles. They are the singular points. When the EE axis moves across the poles, the normal will suddenly changes direction; it flips from the usersÆ viewpoint.
Normally, the preferred pose is the one when the solver is first assigned. So the plane on that one corresponds to the horizontal plane here. Rule A makes sure that the chain will stay on the plane if one moves the goal on the plane.
Rule B means that, when you move the goal along the great circle vertical to the equator, the chain will stay vertical, except when it passes through the poles, which are the singular points of this map.
So far, we have described things as if the whole world comprises only IK elements. In practice, the IK chain and goal can sit at points of separate transformation hierarchies. Ultimately, we need to map the position of the end effector that is described in the world to a point on the sphere. Depending how the sphere is mounted relative to the end effector position, the readings of latitude and longitude are different. The parent transformation space that this sphere is to be placed in is called the Swivel Angle Parent Space, or Parent Space when the context is clear.
The parent space has to be invariant with regard to the IK parameters. Right now, we provide two choices:
Start Joint: The Swivel Angle Parent Space is the same as the parent space of the Start Joint.
IK Goal: The Swivel Angle Parent Space is the parent space of the IK Goal.
If both the start joint and the goal are rooted directly at the world, the choice of Parent Space does not give rise to any difference. In the following example, the start joint is parented to object A.
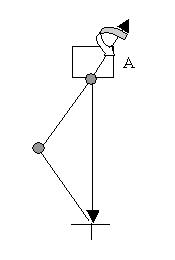
Start joint parented to A
Assume this is the pose when the IK solver is assigned. So, this is the preferred pose. The plane on that the joints are laid out is the horizontal plane of the (Zero Plane Map) sphere.
A: Parent Space is Start Joint.
In this case the sphere is parented to A. If A is rotated about the drawn axis, the sphere will rotate together with it. The goal is in a separate transformation hierarchy. It will remain and the end effector sticks to it due to the IK solve. Since the (plane) normal is fixed to the sphere, it rotates with A, too. Therefore, the whole chain appears to be rotated together with the parent object.
B: Parent Space is IK Goal.
Suppose that the goal is parented to the world. In this case, the sphere is parented to the world and, hence, stays fixed. Since the normal is fixed to the sphere, the chain will appear stationary when A is rotated.
In the following example, we look at a case where there exists a rotation in the parent space when the IK solver is assigned.
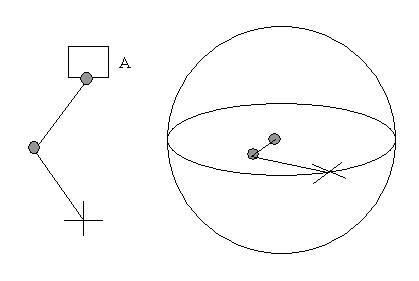
Rotation in parent space
Parent A contains a rotation of 90 degrees. This is an abstraction of the case when a user creates four bones without IK solver and later assigns an IK solver from Bone2 to Bone4. If we parent the chain directly to world, it would appear as shown in the right figure: the solver plane becomes horizontal.
A: Parent Space is Start Joint.
The sphere is mounted after the rotation of A and therefore the ôhorizontal planeö coincides with the chain plane as shown in the viewport. The singular points are perpendicular to the Start Joint with regard to the plane. When the goal/end effector is moved on the plane, it will never hit the singular points and flip.
B: Parent Space is IK Goal.
Again, we assume that the parent space of the goal is the world. The ôhorizontal planeö of the sphere becomes horizontal, as shown in the right figure. The singular points, the poles, are on the plane that joints are laid out. Therefore, when users move the goal/end effector left to right, or the other around, the end effector will move across the singular point and flip.
A problem of B is that the figure on the right is never shown to the user. They have to envision it in order to understand the flipping.